经典排序算法

## 什么是排序？

### 样例

输入：

```txt
4 2 3 5 1
```

输出

```txt
1 2 3 4 5
```

### 更大一点的

输入：

```txt
84 85 3 36 29 22 34 33 66 9 1 100 22 77 42 61 21 70 28 43 63 10 95 33 33 28 75 24 74 77 84 94 70 54 13 3 52 81 35 42 99 100 92 48 63 11 98 49 10 98
```

输出：

```txt
1 3 3 9 10 10 11 13 21 22 22 24 28 28 29 33 33 33 34 35 36 42 42 43 48 49 52 54 61 63 63 66 70 70 74 75 77 77 81 84 84 85 92 94 95 98 98 99 100 100
```

### 模板题

- [排序](http://www.nekko.cn:1234/problem/200)
  - $n\le 10$，支持 $O(n!)$ 等复杂度的做法。
  - $n\le 1000$，支持 $O(n^{3\over 2}), O(n^2)$ 等复杂度的做法。
  - $n\le 100000$，支持 $O(n\log n), O(n\log^2 n)$ 等复杂度的做法。

----

## 什么是排序算法？

- 算法是将可能的输入转化为预期输出的过程。
- 排序算法是将一个数列转化为有序数列的过程。

----

## 经典排序算法

1. 冒泡排序
2. 选择排序
3. 插入排序
4. 希尔排序
5. 归并排序
6. 快速排序
7. 堆排序
8. 计数排序
9. 桶排序
10. 基数排序

----

## 冒泡排序 Bubble Sort

### 流程

1. 重复遍历待排序数组，比较每对相邻元素；
2. 如果前者大于后者，则交换；
3. 每一遍历结束后，当前未排元素中的最大值会“沉”到末尾；
4. 上述过程，直至无需交换为止。

### 伪代码

```pseudo
function bubbleSort(A):
  n = length(A)
  for i from 0 to n-2:
    for j from 0 to n-2-i:
      if A[j] > A[j+1]:
        swap A[j], A[j+1]
```

### 复杂度

- 最坏情况（完全逆序）下为 $O(n^2)$
- 最好情况（已近乎排序）下为 $O(n)$
- 平均复杂度为 $O(n^2)$

----

## 选择排序 Selection Sort

### 流程

1. 在未排序部分中找最小（或最大）元素；
2. 与当前起始位置交换；
3. 缩小未排序部分继续上述步骤。

### 伪代码

```pseudo
function selectionSort(A):
  n = length(A)
  for i from 0 to n-2:
    minIndex = i
    for j from i+1 to n-1:
      if A[j] < A[minIndex]:
        minIndex = j
    swap A[i], A[minIndex]
```

### 复杂度

- 不管数组初始状态如何，比较次数固定，时间复杂度始终是 $O(n^2)$

----

## 插入排序 Insertion Sort

### 流程
1. 将数组分为已排序和未排序两部分；
2. 依次取未排序的元素，插入到已排序部分正确位置；
3. 重复直到完成。

### 伪代码

```pseudo
function insertionSort(A):
  for i from 1 to length(A)-1:
    key = A[i]
    j = i - 1
    while j >= 0 and A[j] > key:
      A[j + 1] = A[j]
      j = j - 1
    A[j + 1] = key
```

### 复杂度

- 最坏情况（完全逆序）下为 $O(n^2)$
- 最好情况（已近乎排序）下为 $O(n)$
- 平均复杂度为 $O(n^2)$

----

## 希尔排序 Shell Sort

### 流程

1. 按增量将元素划分为多个子序列；
2. 对每子序列执行插入排序；
3. 缩小增量重复步骤，最后增量为 1 时完成排序。

### 伪代码

```pseudo
function shellSort(A):
  n = length(A)
  let gaps = [gap1, gap2, ..., 1]  # 递减
  for gap in gaps:
    for i from gap to n-1:
      temp = A[i]
      j = i
      while j >= gap and A[j - gap] > temp:
        A[j] = A[j - gap]
        j = j - gap
      A[j] = temp
```

### 复杂度

- [维基百科](https://zh.wikipedia.org/wiki/%E5%B8%8C%E5%B0%94%E6%8E%92%E5%BA%8F)
- 最坏情况 $O(n \log^2 n)$
  - [Proof](https://oi-wiki.org/basic/shell-sort/)

----

## 归并排序 Merge Sort

### 流程

1. 递归将数组对半分直到子数组长度为 1；
2. 合并两个已经排序的子数组；
3. 合并继续上溯直到整个数组排序完毕。

### 伪代码

```pseudo
function mergeSort(A):
  if length(A) ≤ 1:
    return A
  mid = length(A) // 2
  left = mergeSort(A[0:mid])
  right = mergeSort(A[mid:])
  return merge(left, right)

function merge(L, R):
  result = []
  while L not empty and R not empty:
    if first(L) ≤ first(R):
      append first(L) to result; remove first(L)
    else:
      append first(R); remove first(R)
  append remaining L or R to result
  return result
```

### 复杂度

- 时间复杂度稳定为 $O(n \log n)$
- 需 $O(n)$ 额外空间

----

## 快速排序 Quick Sort

### 流程

1. 从数组中选择一个枢轴（pivot）；
2. 分区：小于 pivot 的放左边，大于的放右边；
3. 递归排序左右子区。

### 伪代码

```pseudo
function quickSort(A, lo, hi):
  if lo < hi:
    p = partition(A, lo, hi)
    quickSort(A, lo, p - 1)
    quickSort(A, p + 1, hi)

function partition(A, lo, hi):
  pivot = A[hi]
  i = lo
  for j from lo to hi-1:
    if A[j] < pivot:
      swap A[i], A[j]
      i = i + 1
  swap A[i], A[hi]
  return i
```

- 最坏情况下（如已排序数组选枢轴不当）退化为 O(n²)  
- 期望复杂度为 O(n log n)

----

## 堆排序 Heap Sort

### 流程

1. 构建最大堆；
2. 将堆顶（最大）元素与末元素交换，缩减堆范围；
3. 重新调整堆；
4. 重复步骤直到排序完成。

### 伪代码

```pseudo
function heapSort(A):
  buildMaxHeap(A)
  for i from length(A)-1 downto 1:
    swap A[0], A[i]
    heapify(A, 0, i)

function buildMaxHeap(A):
  n = length(A)
  for i from floor(n/2)-1 downto 0:
    heapify(A, i, n)

function heapify(A, i, heapSize):
  largest = i
  left = 2*i + 1
  right = 2*i + 2
  if left < heapSize and A[left] > A[largest]:
    largest = left
  if right < heapSize and A[right] > A[largest]:
    largest = right
  if largest ≠ i:
    swap A[i], A[largest]
    heapify(A, largest, heapSize)
```

### 复杂度

- 构建堆后每次堆调整最坏是 O(log n)，因此最坏也是 O(n log n)

----

## 计数排序 Counting Sort

### 流程

1. 找出待排序数组中最大值和最小值；
2. 统计各数值出现次数，存入计数数组 C；
3. 让 C 累加，得到每个值的最终位置；
4. 反向遍历原数组，将元素放入输出数组，更新 C。

### 伪代码

```pseudo
function countingSort(A):
  find minVal and maxVal in A
  k = maxVal - minVal + 1
  C = array of zeros size k
  for x in A:
    C[x - minVal] += 1
  for i from 1 to k-1:
    C[i] += C[i - 1]
  B = output array same size as A
  for i from length(A)-1 downto 0:
    x = A[i]
    B[C[x - minVal] - 1] = x
    C[x - minVal] -= 1
  return B
```

### 复杂度

- 时间和空间均为 $O(n + k)$，$k$ 为键值范围大小

----

## 桶排序 Bucket Sort

### 流程

1. 根据数据范围和分布创建若干桶；
2. 将元素分布到对应桶中；
3. 对每个桶内部排序（如插入排序等）；
4. 合并所有桶里的元素得到结果。

### 伪代码

```pseudo
function bucketSort(A, bucketCount):
  create buckets[0..bucketCount-1] as empty lists
  for x in A:
    idx = mapping(x)
    append x to buckets[idx]
  for each bucket in buckets:
    sort(bucket)
  return concatenation of all buckets in order
```

### 复杂度

- 若所有元素落在一个桶内，最坏成为 $O(n^2)$

----

## 基数排序 Radix Sort

### 流程

1. 将整数补齐位数；
2. 从最低有效位（LSD）或最高位（MSD）开始，对每一位排序（如使用计数排序）；
3. 位排序完成后，整个序列即是有序的。

### 伪代码

```pseudo
function radixSortLSD(A, d):
  for digit = 1 to d:  # 从最低位到最高位
    A = stableSortByDigit(A, digit)
  return A
```

### 复杂度

- 最坏情况和平均相同，复杂度为 $O(n·k)$，$k$ 为位数

----

## 稳定性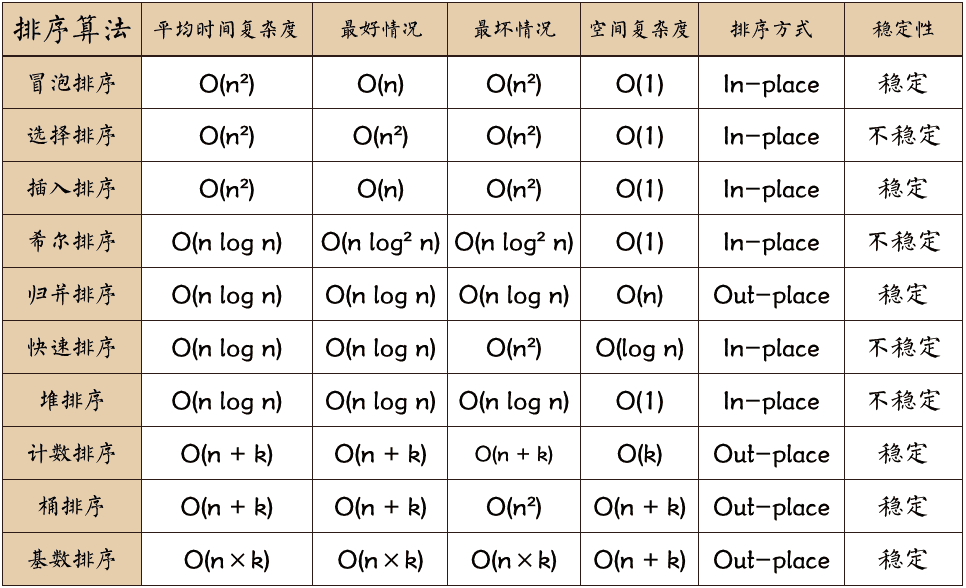

![](https://www.runoob.com/wp-content/uploads/2019/03/sort.png)

----

## 参考资料

- [十大经典排序算法](https://www.runoob.com/w3cnote/ten-sorting-algorithm.html)
- [排序算法可视化演示器](http://www.nekko.cn:1234/visual/sort.html)